Arnold Vissière (1858-1930)

RECHERCHES SUR L'ORIGINE DE L'ABAQUE CHINOIS

et sur sa dérivation des anciennes fiches à calcul
Bulletin de géographie historique et descriptive, Paris, 1892, pages 54-80.

• "Nous nous bornerons, dans cette étude, à donner une courte description du souan-p'an [abaque, boulier], qui suffise à en faire comprendre le principe, puis nous demanderons aux livres scientifiques chinois avec quels instruments les anciens mathématiciens de l'empire du Milieu effectuaient leurs calculs, avant qu'ils ne connussent l'abaque, et nous nous efforcerons de déterminer la date approximative à laquelle a commencé l'usage de ce dernier."

Extraits : L'abaque - Les anciennes fiches à calcul - La similitude fiches/abaque
Feuilleter
Télécharger

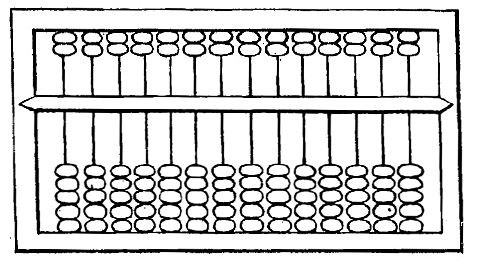
L'abaque chinois est formé d'un plateau ou caisse rectangulaire en bois, dont les deux rebords les plus longs soutiennent une série de broches partageant sa surface en autant de lignes ou colonnes parallèles. Sur chacune de ces broches sont enfilées sept boules mobiles, légèrement aplaties, pouvant se rapprocher ou s'éloigner d'une barre transversale, qui divise la machine en deux parties inégales, de telle façon que deux boules de chaque colonne demeurent toujours au-dessus et cinq au-dessous de cette barre de séparation.

Dans les abaques ordinaires, les colonnes sont au nombre d'une douzaine. Ce chiffre est porté à vingt, trente, ou plus, selon les besoins du calculateur.

Les règles fondamentales sur lesquelles repose le maniement de l'abaque sont les suivantes :

1° Chacune des boules situées au-dessus de la barre transversale équivaut aux 5 boules qui se trouvent au-dessous, sur la même colonne verticale ;

2° La valeur relative des colonnes croît de 10 en 10, de la droite vers la gauche. Sur deux colonnes voisines, une boule de gauche vaudra donc 10 de la rangée de droite.

Veut-on marquer sur l'abaque un nombre quelconque ? On commencera par écarter de la barre transversale, pour les rapprocher des bords inférieur et supérieur de la machine, toutes les boules. Puis on ramènera contre cette barre autant de boules qu'il sera nécessaire, étant donnée la valeur relative des colonnes, pour figurer le nombre donné.

Or, il est bon de remarquer que le choix de la colonne des unités sur le souan-p'an ne dépend que de la volonté de l'opérateur, qui pose ses nombres sur la machine suivant les exigences des données. Cependant, il arrive souvent qu'un caractère de cuivre soit fixé, comme aide-mémoire, sur la barre transversale et, pour ainsi dire, à cheval sur chaque colonne, pour en indiquer la valeur : unités, dizaines, centaines, milliers, myriades, etc., ou la dénomination : piculs, livres, boisseaux, pieds, pouces, etc.

Ceci dit, pour représenter le nombre 1, on élèvera une seule des boules inférieures de la colonne que l'on aura choisie comme celle des unités. Pour marquer 2, 3 ou 4, on en élèvera, de la même façon, deux, trois ou quatre. S'il s'agit de figurer 5, on abaissera une des boules supérieures de la même rangée, tandis que 6, 7, 8 et 9 se porteront en abaissant une boule supérieure valant 5, et en élevant, en même temps, une, deux, trois ou quatre boules inférieures, formant le complément du chiffre proposé. Les dizaines, centaines, etc., s'inscrivent de même, à leurs colonnes respectives.

Sur l'abaque représenté par la figure ci-dessous, la colonne A ayant été adoptée comme celle des unités, on a porté le nombre ; 123 millions, 456 mille, 789 unités.

Une colonne laissée vide sur l'abaque remplace notre zéro. Si le nombre donné contient une fraction décimale, on l'inscrit à droite de la rangée des unités. Supposons que celle-ci ait été choisie en B, le nombre ci-dessus deviendra : 123 mille, 456 unités et 789 millièmes.

Nous avons vu que 9 était figuré sur l'abaque par une seule boule supérieure valant 5, et quatre inférieures formant le complément du nombre. Cinq boules suffisent, par conséquent, à la notation numérique. Cependant, chaque colonne contient sept boules, valant en tout 5. La raison de cette disposition est que, pour effectuer sur l'abaque une division, il est souvent indispensable de poser, sur une même colonne, provisoirement, un nombre supérieur à 9. Pour les trois premières opérations, cinq boules suffiraient à chaque rangée. Dans ce cas, néanmoins, le calcul peut être simplifié si l'on marque temporairement, sur une même colonne, un résultat partiel dépassant 9.

Certains abaques japonais ne contiennent qu'une boule, à chaque colonne, dans le compartiment supérieur, et cinq au-dessous.

Les colonnes de l'abaque russe portent dix boules d'égale valeur, aussi n'a-t-on pu, jusqu'ici, au dire de Goschkewitsch, imaginer aucun moyen pratique pour y effectuer des divisions. L'opérateur se voit contraint de mettre en œuvre plusieurs abaques à la fois.

Les boules de l'abaque portent, en chinois, le nom de tchou « perles », ou de tse « fils, enfant, grains ». Dans la langue parlée, on les appelle souan-p'an tchou-tse. La barre transversale porte la désignation de leang « poutre », et aussi de tsi-leang « colonne vertébrale », dont elle rappelle à l'œil des Chinois l'image, pourvue des broches qui la traversent, comme l'échine de l'homme se rattache à une double ligne de côtes.

Les colonnes sont appelées wei « positions », hang « lignes, rangées », ou tang « échelons, barreaux ». Le côté gauche de l'abaque en forme l'« avant » ts'ien, tandis que la droite en est l'« arrière » heou. Il en résulte qu'« avancer » un nombre, tsin, signifie le porter vers la gauche, tandis qu'on le « recule », t'ouei, en le plaçant plus à droite. Par le même motif, chang, le « haut », et hia, le « bas » désignent plus souvent la gauche et la droite de l'abaque que ses deux sections au dessus et au-dessous de la barre transversale.

On dit « monter », chang, un nombre sur l'abaque, pour l'y marquer. S'il s'agit de l'éliminer, on se sert de l'une ou de l'autre des expressions : t'ouei « repousser », k'i « enlever », tch'ou « éliminer », et k'iu « chasser ».

Un nombre étant porté sur l'abaque, sa première colonne est appelée sa « tête », cheou, ou t'eou. Sa dernière rangée forme sa « queue », wei, ou sa « fin » mo. On « remonte » cheng ce nombre, quand on en suit les colonnes ou chiffres de la droite vers la gauche ; on le « descend » kiang, dans le cas contraire.

La colonne que l'on considère, sur laquelle on opère, reçoit la dénomination de « corps », chen, synonyme de pen-wei « la colonne même ».

Une similitude indéniable existe entre les deux systèmes des fiches et de l'abaque, et nous sommes tout naturellement porté à admettre que le second n'est qu'un perfectionnement du premier. En effet, le trait caractéristique de l'abaque chinois, qui le différencie tout d'abord des instruments similaires usités en Europe est la répartition des boules en deux séries superposées, la boule supérieure valant 5. Cette boule ne joue-t-elle pas précisément le même rôle que la fiche qui couronne tous les nombres au-dessus de 5 dans la vieille méthode ? On marque aujourd'hui sur l'abaque : [cf. (A) ci-contre], comme, sous les Han, sous les T'ang ou sous les Song, on rangeait sur la table les baguettes arithmétiques suivantes : [cf. (B) ci-contre].

Nous ne savons malheureusement pas d'une façon précise quel fut l'homme ingénieux qui sut fixer, en quelque sorte, les anciennes fiches sur des broches, qui en distinguèrent les valeurs relatives, en les remplaçant par des boules mobiles le long de ces colonnes et qu'un arrêt transversal en bois partagea en deux séries, de la même manière que les fiches se distribuaient en horizontales et en verticales. Peut-être fut-ce Kouo Pe-yu.

Les premiers abaques ne durent comprendre qu'une seule boule dans leur partie haute au lieu de deux, et n'en porter que quatre dans leur partie inférieure. Les calculs, déjà singulièrement simplifiés par la fixation des boules sur les broches, le furent encore par l'addition d'une boule supplémentaire en haut et en bas, ce qui permet d'effectuer plus aisément les notations intermédiaires et les résultats partiels. La division s'en trouve grandement facilitée, comme nous l'avons déjà vu.

Cependant, l'adoption de l'abaque changea la forme des opérations. Autrefois, dans une multiplication, on plaçait le groupe de fiches représentant le multiplicateur en haut et le multiplicande en dessous. Le produit se marquait plus bas. L'abaque, au contraire, ne peut offrir qu'une ligne horizontale de nombres. On porta donc le multiplicateur sur les colonnes de droite et le multiplicande sur celles de gauche. Quant au produit, il s'inscrit à la place du multiplicande, dont il chasse les boules au fur et à mesure que l'opération se poursuit.

Voici un modèle de multiplication à l'aide des fiches, que nous trouvons dans Yang Houei : [cf. (C)]

Sur l'abaque, on porte : [cf. (D)]

et, l'opération une fois effectuée, l'abaque présente les indications suivantes : [cf. (E)]

L'exemple ci-dessus montre à la fois l'affinité et les différences obligées des deux systèmes.

De tout ce qui précède semble résulter ce fait, qui n'est indiqué nulle part, mais qui mériterait de l'être, — que l'abaque est comme le résumé, la reproduction sous une forme qui le rend plus maniable et rapide de l'ancien procédé des fiches arithmétiques. Et que penser, dès lors, de cette assertion qui veut que l'abaque ait été inventé dans les premiers âges de la monarchie chinoise, par Li-cheou, ministre de Houang-ti, l'empereur Jaune, qui vivait 2.600 ans avant l'ère chrétienne, ou par Tcheou-kong, antérieur à Confucius ? En Chine, des lettrés ignorants ont seuls pu le prétendre, faute d'avoir examiné les sources qui pouvaient les instruire. Le témoignage de Siu Yo demande confirmation, et nous ne savons que penser de sa planchette à boules. Mei Wen-ting ne la prenait sans doute pas au sérieux. L'histoire se borne à dire que Li-cheou, sur l'invitation de Houang-ti, inventa le calcul, c'est-à-dire, peut-être, les fiches arithmétiques. Quant à Tcheou-kong, il s'occupa fort de mathématiques et d'astronomie, notamment des Neuf chapitres, qui résument, pour les Chinois, la géométrie, l'arithmétique, l'algèbre et la trigonométrie, mais nous ne voyons nulle part qu'il se soit servi d'un abaque. Il convient donc de nous ranger à l'opinion des mathématiciens chinois, et, — tout en admettant qu'un abaque rudimentaire ait pu exister sous les Song méridionaux, — de voir dans la machine actuelle, parfaite en son genre, une création de la seconde moitié du XIVe siècle.